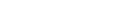Main Features
-

WORDPRESS APP
Inspiration strikes anytime, anywhere. WordPress: at your fingertips.
-
Responsive Website
Provide all smart device optimized view.
-

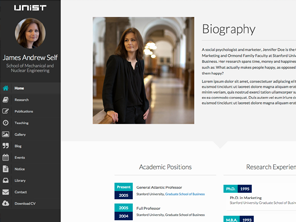
Various WordPress Themes
Full featured modern website themes and various designs to be updated.
-

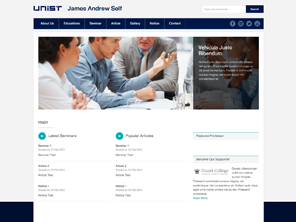
Better SEO Optimization.
Automatically optimize your WordPress blog for Search Engines such as Google.
-

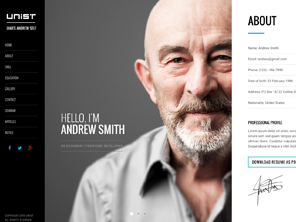
SNS Share
Add various social networking share buttons to your website, including; Facebook, Twitter and Google+.